Has A Mind for Numbers by Barbara Oakley been sitting on your reading list? Pick up the key ideas in the book with this quick summary.
Do you find your head spinning when you are asked to work with numbers and equations? You are in good company. The author, Barbara Oakley, generally hated math. Sometimes she even failed her school math and science courses. Yet she discovered she needed advanced math skills to pursue her dream career after graduation. Now a professor in engineering, Oakley shares her secrets with easy methods and fun tricks to help you excel at math and science in her book A Mind for Numbers.
In A Mind for Numbers, you’ll also learn;
- having a hard time learning? – take a nap
- why playtime is as important as work time
- why being a genius isn’t so great
A Mind for Numbers Key Idea #1: Two Ways of Thinking
Our brains can switch between two kinds of functions or networks. Sort of like a flashlight with two settings. One setting intensely focuses the beam on one very small area. The next setting spreads its light more broadly, but less powerfully. Our brains work in a way similar to this.
We might concentrate on information that’s already firmly held in our minds. This is focused mode thinking. focused mode thinking is generally used for concepts with which we are already familiar and comfortable.
Because we use focused mode to solve problems using rational thought and analysis, it is essential to the study of math and science.
An example of focused mode thinking happens when you multiply numbers (as long as you can already multiply). Or you might use focused mode thinking to incorporate last week’s verb conjugation in the study of language.
Our second way of thinking happens when you relax your attention and let your mind wander a bit. This is called is diffuse mode thinking. This type of thinking helps us build the “big picture” of a new concept.
Because diffuse mode thinking allows you to use new insight to look into problems you’ve been struggling with, it is also important for learning math and science.
It’s generally better to not focus on one thing when trying to grasp a new concept. Use your diffuse mode of thinking to see the “big picture” instead.
Consider this sentence: Thiss sentence contains threee errors. A focused approach easily identifies the first two errors – in spelling.
But what about the third error? The third error only becomes clear when we use the diffuse thinking approach to consider the sentence as a whole. The entire sentence is untrue because there is no third error. Both types of thinking have their purposes.
A Mind for Numbers Key Idea #2: Learning Fundamentals
We tend to switch back and forth between the focused and diffuse modes as we go about our daily routines. While we can be in one or the other, we are never in both at the same time consciously.
It is important for our learning process to switch between modes as the process allows for better understanding and problem-solving.
We nearly always need periods of time when we aren’t consciously thinking about a specific issue to tackle intellectual problems and learn new concepts. This is when our diffuse mode comes into play.
After this interlude, we can consolidate the bigger-picture insights we’ve gained from diffuse mode when we turn our attention back to the problem.
During the course of learning, thoughts are processed in one mode of thinking, then the information is sent to the other mode. This is this essential volleying back and forth of information that allows us to use both modes to work toward a solution.
Another essential element in the learning process is sleep. Your consciousness is similar to your body in this way. You can’t grow your muscles bigger by lifting weights constantly. You must take time to rest and recover before they’re used again. When you rest between weight-lifting sessions, your body uses that time to build strong muscles.
Learning is the same. Periods of rest to help our brain to refresh and reinvigorate our thinking.
Sleep clears away toxic products that are created in our brains when we’re awake for too long, thus keeping our brain healthy. This protective function makes sleep a vital part of learning and memory. Also, research has shown that there’s a higher chance we’ll dream about learning material we review right before sleep, and dreaming about it can enhance our understanding.
So try switching your mode of thinking if you get frustrated with something - or taking a nap.
A Mind for Numbers Key Idea #3: Gaining Expertise
The human mind is extraordinary in its capacities. Did you know your mind doesn’t have to process each individual tree for you to see the entire forest?
We call this mental ability chunking. We use this important part of learning at the beginning of our path toward gaining expertise in math and science.
Pieces of information that have a common meaning when connected together are called chunks. An example of this would be the word pop, where we take the letters p, o, and p and put them together into one conceptual chunk.
Our brain runs more efficiently when we chunk information. Once an idea or concept has been chunked, we’ve got the main meaning and we don’t need to remember each underlying detail.
As we continue to learn, we are building a chunked, mental library of concepts we can refer to. When solving puzzles, we train our brains not only to recognize specific problems but to understand different types and classes of problems also. These references help us to solve new puzzles much more quickly in the future.
While learning, you can help build new chunks of information by recalling the material you’re trying to learn. Recall is when you retrieve the main ideas of your learning material mentally. It keeps the chunking process going.
Focusing your attention on the basic ideas, then going over them repeatedly is the best way to build chunks. Understanding the new chunks in the context of other information you are already familiar with is also necessary.
Just looking at the solution won’t help you understand a math problem. In order to really grasp it, you must weave the concepts of the idea into the web of concepts and chunks that already exist in your brain.
When you’re studying, force yourself to work your way through problems and solve them. Don’t just passively reread information – actively practice recalling it.
A Mind for Numbers Key Idea #4: Defeat Procrastination
How do you prevent pain your calf muscles during a big marathon? That’s easy, you practice – a lot. Similarly, if you want to compete in math and science, you can’t procrastinate either.
It’s very tempting to procrastinate, so prevention is important. We tend to procrastinate when things are difficult, make us feel uncomfortable, or are just plain boring. Because we think procrastinating offers temporary relief from an unappealing present, it’s something we can all easily succumb to.
You’ve got to discipline yourself against procrastination if your desire is to excel in math and science.
Learning math and science can be considered this way: brief study sessions help you to lay the “bricks” of information in the mortar, but then you need time in between those sessions for the mental “mortal” to solidify.
This means you can’t cram information into your brain at the last minute. You need to spread your learning process over a long period of time.
To prevent procrastination, focus on the process, rather than the product, of your learning.
The process refers to the time you actually spend doing something. For example, you might say “I’m going to study for the next 20 minutes.”
The product is the outcome of that time spent, such as a finished homework assignment.
Focusing on the process of learning allows you to relax and enjoy your task more. Because you’re less focused on quickly getting the end result, you won’t judge yourself as harshly.
Sometimes we avoid trying to reach a particular result because the finished product is so challenging to reach. We fear failure or we’re uncomfortable with the difficulty, so we don’t try at all. This is a kind of procrastination and it can be prevented by focusing on the process and not worrying about the end result.
As you get accustomed to focusing on the process you’ll enjoy learning more and you’ll find it gets much easier to avoid procrastination.
A Mind for Numbers Key Idea #5: Mental Tricks
David Allen, the management specialist, stated, “To a great degree, the highest-performing people I know are those who have installed the best tricks in their lives.”
You can use many simple, but effective, mental tricks when learning.
Try putting yourself in new surroundings. Experiment and learn where you’re the most productive. Is it a busy coffee shop or a quiet library? According to research, a special place reserved for working is especially helpful for preventing procrastination.
Another helpful concept is Mindfulness training. Similar to meditation, mindfulness training requires you to learn to ignore distracting thoughts, letting them drift past without paying them any attention. You can count down numbers to meditate as focusing on counting relaxes you while training you to be mindful.
You might also try reframing your focus. When you shift your attention from something negative to something positive you are reframing your focus, which helps you adjust your whole attitude.
A helpful example of reframing your focus for those who have trouble getting up in the morning would be to think about how good your breakfast will be rather than how tired you are.
Keeping reasonable, achievable to-do lists is one of the most effective learning tricks. After all, your life is constructed of your habits and the list helps you gain control them.
You could write a brief to-do list once a week, or even every day. This way, you’ll be able to worry less about the details and step back, look at the bigger picture, and set your priorities.
Another great tool to help you stay on track is a planner journal. It’s important to remember that “play” is just as important as work when scheduling your time. Because it will take away your reasons to procrastinate, planning for “play” helps you avoid this unhealthy habit.
A Mind for Numbers Key Idea #6: Memorization
When information is meaningful to us, we learn and recall it much more easily. So make your memorization process an exercise in creativity.
Suppose you need to remember Newton’s second law: f = ma for a test. Force is related to mass and acceleration in this law. Here’s the creative part: the letter f could stand for fly, m for mule and a for apples. If you want your mule to fly faster, feed it more apples.
Creating metaphors is one of the most effective memorization techniques because it lets you see how one thing is similar to another.
It helps you to understand electrical currents, for example, if you visualize them as water. You can think of the voltage pressure on the water.
Because they connect new information to concepts that you already know, metaphors help cement ideas in your mind. As you build more connections, it will become easier to recall concepts and their meanings.
Sometimes it helps to pretend the concept you’re trying to understand is you. Can you imagine that you’re inside of an algebraic equation as the x, or that you are an electron?
Acronyms, another useful tool in memorization, help you by simplifying your learning material.
You can visualize a GRAHAM cracker to help you remember four plants – garlic, rose, hawthorn, and mustard since the first letters of each word abbreviate to GRHM.
A kind of acronym many accomplished academics in many disciplines use is memorable sentences. The first letter of each word in a list that needs to be memorized becomes the first letter of each word in the sentence.
These sentences can even form a story with the meaning of that story making it easier to retain and recall the information.
A Mind for Numbers Key Idea #7: Practice and Persistence
Working alongside other people can be intimidating, especially if they seem to grasp new concepts more quickly than you do. Take heart, sometimes “average” students have advantages when it comes to creativity and work ethic.
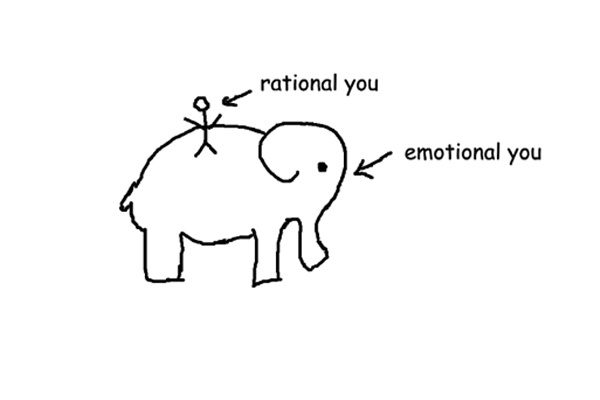
Most people don’t realize that gifted people often have their own set of challenges to face. Smarter people often have a longer working memory, the portion of our memory that holds what we’re currently processing in our mind.
While this may seem like a good thing, a very strong working memory can be so unwavering that new thoughts can’t easily get through. This strong focus can lead smart people to get bogged down on simple problems and overlook simple solutions. Research has shown that smart people may have trouble focusing because they have a higher tendency to lose themselves in complex thoughts.
Would you be surprised to hear that practice and persistence are often more important than intelligence alone?
Our long-term memory is where thoughts are stored to be accessed later. Practice cements memories into this part of our consciousness.
While high-powered working memories are focused on a specific area of the brain, average working memories can get more input from other areas of the brain, like our long-term memory, because they don’t lock in so tightly.
Since these other areas are often the source of creative ideas, we become more creative as we build memory connections by practice.
On the other hand, Persistence in learning allows us to go more deeply into a problem. Persistence leads us to ask the questions necessary for getting the right answers and improves our ability to think independently.
By working hard and practicing diligently, people of average intelligence are capable of achieving the same mental feats as those who are “naturally” gifted.
A Mind for Numbers Key Idea #8: Testing
Rather than being just about measuring how much we know; testing is a powerful learning experience in itself. Studying and preparing for exams are highly important components in the learning process.
Testing doesn’t merely assess learning but facilitates it by improving our ability to retain what we’ve learned. Scientists call this the testing effect.
In 2009, research into the testing effect was conducted by two psychologists by the name of Julie Campbell and Richard Meyer. In their study, two groups of participants were given information they needed to learn via a PowerPoint presentation. One of the groups was tested with a multiple choice question after every few slides, forcing them to recall what they’d just seen.
When given an exam at the end, the participants who’d been given test questions as the presentation went on performed better. This is the testing effect. It’s been shown, even when the test performance is bad, or no feedback is given, the testing effect still occurs.
Testing can also help us deal with anxiety or stress. When it’s under stress, the body puts out chemicals like cortisol, which can cause a racing heart or sweaty palms.
While this may sound unpleasant – even unhealthy, according to research the way we interpret these symptoms makes a big difference. By shifting your focus from fear to excitement and anticipation of success, you can improve your performance.
You can also momentarily turn your attention to your breathing if you’re feeling a bit panicky before a test. Not only will it help you calm down, but deep breathing sends more oxygen to critical areas in the brain.
Although it may not be your favorite activity, all in the all, testing is very useful in learning. By practicing these techniques, you’ll be better able to deal with stress or anxiety in exams, channeling it into productivity.
In Review
The key message in this book:
Anyone can improve their understanding of math and science through diligence and hard work. So work at recalling your learning material, and focus on your learning process. It will be challenging at first, but you’ll be able to achieve great things with practice.
Actionable advice:
Take breaks.
Math and science skills must be built slowly, like muscles. Rest between study sessions, and make sure you get enough sleep. In the long run, it more effective than trying to cram a lot of information into one session.
Suggested further reading: How Not to Be Wrong by Jordan Ellenberg
How Not to Be Wrong gives us a glimpse into the way in which mathematicians think and how their way of thinking can benefit us. The book explains how easy it is to be mistaken when we apply mathematical tools incorrectly, as well as giving advice on how we can find correct solutions.